BioSystems, 30 (1993) 57-63 Elsevier Scientific Publishers Ireland, Ltd.
Construction of the full local similarity map for two biopolymers
A. M. Leontovicha , L. I. Brodskyb and A. E. Gorbalenyac
"A. N. Belozersky Institute of Physical and Chemical Biology, Moscow State University, Moscow, 119899, Russia,
bGendalf Ltd., P.O.Box 135, Moscow, A-190 , Russia and
clnstitute of Poliomyelitis and Viral Encephahtid.es, Russian Academy of Medical Sciences, Moscow region, 142782, Russia
A novel algorithm for construction of complete maps of local similarity for two biopolymer sequences is described. The algorithm is much faster than the related Altschul-Erickson procedure, it is implemented as the Dot-Helix module within the GeneBee package. Performance of the algorithm is exemplified with the analysis of the polyproteins of two poliovirus type 3 strains and its effectivity is compared to the Staden method. Possible applications of the algorithm are briefly discussed.
Introduction
One of the most important problems of analysis of biopolymers (polypeptides and polynucleotides) is the comparison of two primary structures (linear strings of monomers). Two approaches to this problem exist. The first one is the alignment of two monomer sequences. The second one is the construction of the so-called "local similarity map" (dot matrix) which maps pairs of similar fragments of coinciding lengths (without insertions and deletions). One of the major advantages of the latter technique is the avoidance of the fixed gap cost in the sequences under comparison, and the possibility of the search for repeats. On the other hand, the most wide-spread program DIAGON created by Staden (1982) and its modifications are not free from serious shortcomings. They are caused by the existence of two a priori parameters, namely, the length of the compared fragments (so-called "window size") and the fragments similarity level. The most dramatic consequences for the final result are caused by the fixation of the window size. First, it results in the loss of pairs of similar fragments if their length seriously disagrees with the window size, second, it does not allow the exact determination of the boundaries of similar fragments. Thus the maximum possible level of similarity cannot be obtained.
Altschul and Erickson (1986) suggested a novel approach to the construction of the local similarity map for two biopolymers, which is free from these shortcomings of the Staden method. A computer implementation of this algorithm allows one to obtain the so-called full local similarity maps which show all pairs of similar fragments irrespective to their length and in their "natural" boundaries, in which the similarity is maximized. The algorithm is essentially based on the hierarchically organized comparison of two sequences by the Staden method which covers all possible window sizes. This method leads to drastic increase of the required computation time, which does not allow one to use this algorithm in PC-oriented packages.
In the present work we suggest a much more economical procedure for the construction of the full local similarity map, on which DotHelix program for IBM PC is based. Several examples demonstrating advantages of this method are presented. In this paper we develop an approach suggested in (Leontovich et al., 1990).
Method
Definitions
The similarity of a pair of fragments was estimated using similarity matrix of two sequences. It is a rectangular table of the size ò x n whose lines and columns correspond to sequences consisting of ra and n monomers, so that initial monomers correspond to the left upper corner of the matrix and diagonals are directed rightwards down. Each cell (i,j) of this matrix contains the value aij determining the similarity of the i-th and j-th monomers of the given sequences. These values are taken from special monomer similarity matrices. In particular, one of the most widely used amino acid similarity matrices is the Dayhoff matrix (Dayhoff et al., 1983).
Each pair of compared fragments of the similar lengths L situated at positions i, i + 1, . . . , i + L — 1 and j, j + 1, . . . , j + L — 1 respectively corresponds to a diagonal segment consisting of numbers aij, ai+1,j+1, . . . , ai+L-1,j+L-1. Each diagonal corresponds to a "comparison frame" defined by a fixed shift of one sequence relative to the other. The number of different diagonals (that is, the number of possible comparison frames) equals n + ò — 1.
The similarity of these fragments is measured by the normalized sum of ai+l,j+l forming the corresponding diagonal segment (Altschul and Erickson, 1986)
L-1where M and D are respectively the mean and the variance of all ò • n numbers aij in the filled sequence similarity matrix. Thus defined similarity measure we will call power of the corresponding diagonal segment. Since variance of the numerator in formula (1) equals D• L, the power is measured in the standard deviation units (SD).
It is more correct, but much more laborious, to measure the similarity of fragments based not on the power, but on the probability of a random appearance of two fragments with the given similarity in a pair of independent Bernoulli sequences of the same length as the compared biopolymers and with the same monomer frequencies. The smaller is this probability (P), the larger is the similarity. For instance, as a similarity measure we can consider ln P (Staden, 1982; Altschul and Erickson, 1986). For such Bernoulli sequences the similarity measured by the power of the considered fragments is a random variable and, as L increases, its distribution tends to the standard Gauss distribution N(0, 1). Thus for large L there is a correspondence between the power A and the probability P not depending on L and expressed by the formula
this relation gets more exact as L increases.
Altschul and Erickson (1986) suggested to consider for each diagonal the following system of segments: the most powerful segment, the most powerful of segments not intersecting with the first one, the most powerful of segments not intersecting with the first two etc., until the powers of segments exceed some threshold value. Segments of this system correspond to pairs of similar fragments occurring in the same comparison frame. Boundaries of the corresponding fragments are exactly since extending or shortening of fragments by one letter necessarily decreases their similarity (power).
The matrix on which for all diagonals the Altschul-Erickson systems of segments are marked and their powers is set we call the full local similarity map. In this paper we present an algorithm which allows to construct such map much faster than it is done in (Altschul and Erickson, 1986).
The algorithm
Our algorithm is based on the following two lemmas about numerical inequalities. Consider a set of n numbers a 1.. , a n, at least one of which is positive. Denote Aij = å jl=i a l / Ö j-i+1 , in particular, AII =- a ii.
Lemma 1. Let 1 £ i £ j < k £ N, Aij £ 0, Aik > 0. Then Aj+1,k > Aik.
Lemma 2. Let 1 £ i £ j < k < p £ N, Aik > 0, Aik ³ Aip, Aj+1,p ³ Aik. Then Aj+k:k ³ A j+1,ð.
Proof. Proof of Lemma 1 is obvious. Let us prove Lemma 2. Denote
j - i + 1 = r, k - j = t, p - k = r, å
l=1j a
l=Sr,
å
l=j+1k a
l = St, å
l=k+1p a
l = Sr. In these designations conditions of Lemma 2 become
(Sr + St)/ Ö ( r+t) ³ (Sr + St + St ) / Ö ( r+t + t ), (3)
(St + St ) / Ö ( t + t ) ³ (Sr + St ) / Ö ( r+t ) , (4)
Sr + St > 0; (5)
is necessary to prove that
St / Ö t ³ (St + St ) / Ö ( t + t ). (6)
From (3) it follows that
St £ (Sr + St) (Ö ( r+t + t )-Ö ( r+t ))/Ö ( r+t). (7)
From (4) and (7) it follows that
St ³ (Sr + St) Ö (t + t ) / Ö ( r+t ) - Sr ³³ (Sr + St)(Ö (r+t)+Ö (t + t )-(Ö ( r+t +t )/Ö ( r+t). (8)
Applying (7), (8) and (5), we obtain
St / Ö t - (St + St ) / Ö ( t + t ) ³ ³ (Sr + St ) / Ö t( r+t)( Ö ( r+t) +Ö ( t + t ) - Ö ( r+t +t ) - Ö t)>0,
since
(Ö (r + t) +Ö (t + t ))2 = r + 2t + t + 2 Ö (rt + t2 + tt + rt ) >
> r + 2t+ t + 2 Ö (rt + t2 +t ) = (Ö ( r+t +t ) + Ö t)2.
Thus inequality (6), and with it Lemma 2, are proven.
Now we present our algorithm for construction of the full local similarity map, which is based on the above propositions. Consider an arbitrary diagonal of the map. Denote by AT, the power of the diagonal segment [r, s], where r and s are the beginning and the end positions of this segment (if the beginning position r of the segment corresponds to the cell (i, j), then r = min(i,j)). In particular, Arr is the similarity measure for two letters corresponding to the position r. We search for the segment of the maximum power within some diagonal segment [r0, s0 ] ("search zone"). From Lemma 1 it follows that if Àrî rî < Î, then the maximum power segment lies strictly to the right from the position to, and thus the search zone can be shortened by one position r0. Let Àr0 r0 > 0. Denote by s* the minimum s for which the power Aros, as a function of s, changes sign from plus to minus. From Lemma 1 it follows that the maximum power segment lies either entirely to the left or entirely to the right from the position s*, but cannot have this position inside. Thus the current search zone can be divided into two smaller search zones [r0,s*] and [s* + i, s0]. Finally, let for all s (r0 £ s £ s0) the power Aros > 0. Let s+ be the value of s for which the power Aros (as a function of s) reaches maximum. From Lemma 2 it follows that the maximum power segment lies either entirely to the left or entirely to the right from s+ and in this case the search zone also can be divided into two smaller ones [r0,s+] and [s+ +1, s0].
After completion of this procedure a system of diagonal segments id found. Each such segment [r0,s0] satisfies the following condition: for all s, r0 £ s £ s0
Aro,s0 > Aros > 0, Aro so > Asso > 0. (9)
It can be considered as a search zone. Generally speaking, inside it a segment of power larger than Aroso can occur (due to (9) it lies strictly within the segment [r0 , s0)- In order to find it, one should shorten the search zone [r0,s0] by one position at each end, i.e. consider a new search zone [r0 + 1, s0 - 1], and repeat for it the same procedure. It greatly increases the program performance time. However, computer experiments with sequences (both biological and random) demonstrate that more powerful segments inside the search zone occur sufficiently rarely, and even if they do exist, then almost always they are very short (1 or 2 letters). Thus in the procedure implemented in the package this operation of the search zone shortening is not provided.On the other hand, in the program it is possible to increase the average substitution weight (M in formula (1)), which allows one to find such inner more powerful segments (procedure of the increase of the average M is considered in more detail in (Brodsky et al., this volume)).
Results and Discussion
The above described algorithm has been implemented in the program DotHelix which is a part of the package GeneBee intended for IBM PC-compatible personal computers (Brodsky et al., 1992). When the module is entered, a user sets two sequences to be analyzed, a monomer similarity matrix, and a threshold of power, starting from which diagonal segments are considered to be similar (Run Level). When the full local similarity map is constructed, it is possible to analyze maps with higher similarity levels without repeating the procedure. In order to do that, it is sufficient to reset the threshold (Draw Level). This feature provides a possibility to find empirically the level that most fully represents the required information.
An example of analysis by DotHelix is presented on Fig. 1, where gigantic precursor polyproteins of two type 3 polioviruses are considered. Their length is 2206 amino acids and the processing requires approximately two hours on IBM PC AT with tact frequency 10MHz and co-processor Intel 80287 for floating point operations. Local similarity maps for three thresholds (4.0, 4.5, 5.0 SD) are presented. The following characteristic features can be observed: symmetry of the obtained maps, concentration of diagonal segments in some areas (especially on Fig. 1A and IB), and the presence of segments of considerably different lengths on one map.
The similar analysis performed by our version of DIAGON program also exposed symmetry and concentration of segments (Fig. 2). However, the number of diagonal segments on these maps was much smaller (for one threshold level) and all of them had similar length close to the window size.
For both analyses symmetry is explained by high similarity of the two proteins, while concentration of diagonal segments (especially in the right lower corner of the map) is caused by the presence of tandem repeats of various lengths (Gorbalenya et al., 1986). A larger number of segments on Fig. 1 demonstrates that DotHelix can find similar fragments more effectively than the traditional approach. Indeed, more
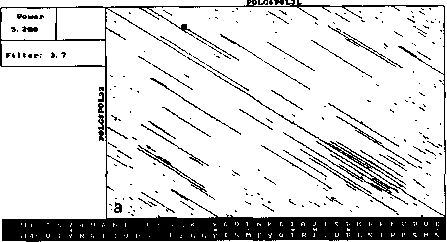
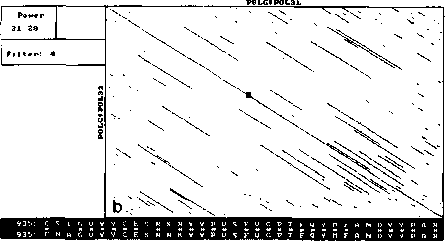
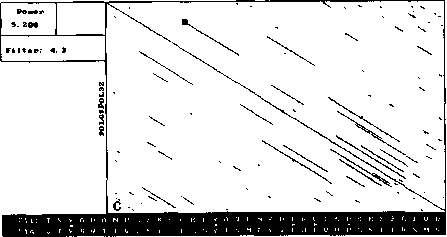
Fig. 1. Full local similarity maps of precursor polyproteins of two poliovirus type 3 strains obtained by DotHelix at the threshold levels 4SD (A), 4..5SD (B) and 5SD (C). Polypro-tein sequences are taken from SwissProt data bank. Black square on the maps denotes the most powerful diagonal segment, its sequence and similarity value are given under the map.

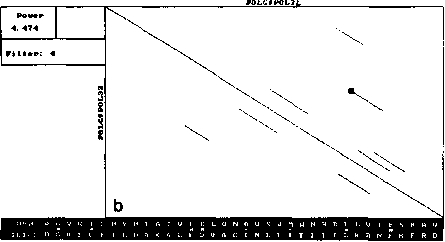
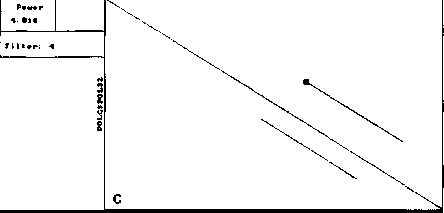
Fig. 2. Local similarity maps for same proteins as in Fig. 1, produced by our version of Diagon for the threshold value 4.5SD and window sizes 21 (A), 99 (B) and 330 (C) amino acids. Other details as in Fig. 1.
detailed analysis of the concentration areas, that is beyond the scope of the present paper, allows one to delineate and characterize the tandem repeats more completely (data not shown).
Thus a single full local similarity map constructed by the presented algorithm provides more information that several local similarity maps on the same threshold level constructed by Diagon. Even more important is the fact that it cannot be obtained by the formal superposition of an arbitrarily large number of traditional maps. So the gain in computer time (construction by Diagon of one map of those presented on Fig. 2 required approximately 4 minutes) cannot compensate for the loss of information.
The most important advantage of the suggested approach as compared to the traditional one is the following. First, the method is more sensitive (all fragments with the given similarity level are discovered). Second, the method is more precise: exact boundaries of similar fragments are found and the power characterizing the similarity of the fragments is computed. These advantages are most visible when long biopolymers with low similarity are compared. Consequently, when a biopolymer is compared to itself, the method can be used for search and analysis of periodicities in its primary structure. We hope also that based on this program it would be possible to develop effective comparison procedures for several sequences. One such method was implemented in the program MA-Tools of GeneBee package (Brodsky et al., this volume).
It should be noted that the algorithm is sound irrespective to the values of the constants M and D, that can differ from the mean and the variance of a,-j. It is considered in more detail in (Brodsky et al., this volume).
Compare our algorithm with the Altschul-Erickson one. The discovered pairs of similar fragments should coincide. However, the computation time is sharply different. Since in the Altschul-Erickson algorithm all possible pairs of fragments of similar lengths are compared, it is essentially equivalent to the total processing by the Staden algorithm for all possible window sizes. Thus the processing time can be estimated. In the presented example it would equal 2206 • 4 = 8824 minutes that is 75 times greater than the processing time of our algorithm (120 minutes).
A natural measure of the effectivity of an algorithm is the number of required elementary operations. Processing of one diagonal of length N by the Altschul-Erickson algorithm requires ~ N2 operations (Altschul and Erickson, 1986). Unfortunately we could not obtain an exact estimate for our algorithm. Unformal considerations lead to the following reasoning. In our algorithm the search zone is divided into two approximately similar new zones. Thus the following conjecture can be made: if independent Bernoulli sequences are compared, then the number of such operations with probability tending to 1 as N ® ¥ has the order N log2 N (a more weak hypothesis is that the order is N1+0(1)). We feel that for biological sequences this estimate holds as well. However, it should be noted that it is possible to construct artificial sequences for which this estimate does not hold and the number of operations has the order N2.
Based on the above conjecture, the ratio of computation times for the Altschul-Erickson and our algorithms is N/log2 N. In the above example N = 2206, N/log2 N = 200. Although this estimate exceeds the experimentally obtained one (75), it is of the same order.
The suggested algorithm finds similar fragments sufficiently well, but in some situations (e.g. when very long sequences are being compared or a bank is scanned) it works too slowly, since all diagonals of the map are processed. In GeneBee package there exists a possibility to exclude from consideration diagonals in which the probability of discovering similar fragments is small (Brodsky et al., 1992). Of course it can cause loss of sufficiently powerful segments.
Finally let us point out a drawback of the suggested program DotHelix. It is related to estimate of similarity of short fragments. As stated above, the correspondence between the power A and the probability P given by formula (2) is not exact for small L. Moreover, numerical experiments demonstrated that for typical in natural proteins amino acid frequencies convergence of the right side of formula (2) to the corresponding probability of the Bernoulli distribution is slow (since for these frequencies the asymmetry and the excess of the distribution of substitution weights are large). As a rule, estimates of similarity based
on computation of power lead to too large values, and the discrepancy is larger for small L. As a result our program tends to map short fragments while possibly missing extended similar fragments. In order to soften this effect it is possible not to consider pairs of very short fragments (e.g. ones with L £ 3 or L £ 4). It is a compromise solution. Currently other, more effective, approaches are considered, one of which has been implemented by I. Ya. Vakhutinsky (personal communication).
References
Altschul, S.F. and Erickson, B.W., 1986, A nonlinear measure of subalignment similarity and its significance levels. Bull. Math. Biol. 48, 617-632.
Brodsky, L.I., Vassilyev, A.V., Kalaydzidis, Ya.L., Osipov, Yu.S., Tatuzov, R.L. and Feranchuk, S.I., 1992, GeneBee: The program package for biopolymer structure analysis, in: Mathematical Methods of Analysis of Biopolymer Sequences, S. Gindikin (ed.) (American Mathematical Society, Providence) pp. 127-140.
Brodsky, L.I., Drachev, A.L., Leontovich, A.M., Feranchuk, S.I., 1993, A novel method of multiple alignment of biopolymers (MA-Tools module of GeneBee package). This volume.
Dayhoff, M.O., Barker, W.C. and Hunt, L.T., 1983, Establishing homologies in protein sequences. Meth. Enzymol. 91, 524-545.
Gorbalenya, A.E., Donchenko, A.L. and Blinov, V.M., 1986, A possibility of the common origin of poliovirus proteins with different functions. Molekulyanaya Genetika no.l, 36-41 (in Russian).
Leontovich, A.M., Brodsky, L.I. and Gorbalenya, A.E., 1990, Construction of a complete map of local similarity for two biopolymers (program DotHelix of the GeneBee package). Biopolimery i Kletka 6, no. 6, 14-21 (in Russian).
Staden, R., 1982, An interactive graphics program for comparing and aligning nucleic acid and amino acid sequences. Nucl. Acids Res. 10, 2951-2961.