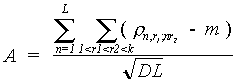
Л. И. Бродский, А. Л. Драчев, А. М. Леонтович
НОВЫЙ МЕТОД МНОЖЕСТВЕННОГО ВЫРАВНИВАНИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ БИОПОЛИМЕРОВ
(ПРОГРАММА
H-AIign ПАКЕТА GenBee )В работе предложен новый алгоритм множественного выравнивания биологические последовательностей. В этом алгоритме вначале на основе метода
DotHelix строятся консенсусные участки в данном наборе последовательностей разной толщины и разной степени сходства, а затем из этих консенсусов составляются цепочки, согласованные с порядком букв в последовательностях, и такие цепочки являются каркасами выравниваний. На основе алгоритма на языке Си написана программа H-Align из пакета GenBee. Рассмотрен модельный пример, иллюстрирующий эффективность предложенного алгоритма.Введение.Как известно, процедура выравнивания широко используется при анализе первичных структур биополимеров. Такая процедура применяется, например, при поиске функционально важных участков белков или молекул ДНК/РНК, при построении филогенетических деревьев и т. д.
Алгоритмы выравнивания, в частности множественного, можно разбить на две основные группы: одноэтапные, оптимизирующие сразу все выравнивание, и двухэтапные. В двухэтапной процедуре на первом шаге находится достаточно большое количество наборов сходных между собой фрагментов из разных последовательностей, а на втором — из этих наборов составляются непротиворечивые цепочки, лучшие из которых и являются альтернативными выравниваниями.
Алгоритмы первой группы, как правило, базируются на процедурах динамического программирования (типа
Нидельмана — Вунша [1, 2]) и требуют назначения величины штрафа за введение пробелов в выравненные последовательности (соответствующих делециям или вставкам остатков). Результат выравнивания существенно зависит от величины штрафа, но в то же время нет никаких сколько-нибудь серьезных оснований для выбора этой величины. Другой недостаток одноэтапных алгоритмов — это то, что обычно в них множественное выравнивание делается последовательно: сначала выравниваются две самые близкие последовательности, затем эта пара как целое выравнивается с третьей, затем тройка как целое выравнивается с четвертой и т. д. Если на одном из шагов выравнивание в каком-то месте было сделано неудачно, то в дальнейшем в этом месте оно будет все более искажаться.Основной недостаток существующих методов второго типа — это грубость процедуры поиска “консенсусов” наборов сходных между собой фрагментов последовательностей. Некоторые из реально существующих консенсусов могут быть пропущены, и вместе с тем границы найденных консенсусов определяются недостаточно точно.
В представляемом ниже алгоритме, относящемся ко второй группе методов, консенсусные участки, по нашему мнению, ищутся более полно
и точно, чем обычно. Наш метод исходит из построения попарных карт локального сходства и основан на алгоритме DotHelix [5].Методы. Пусть имеется несколько последовательностей биополимеров (например, белков). Результат их выравнивания представляет собой набор последовательностей одинаковой длины. Каждая последовательность из набора получается за счет внесения пробелов в соответствующую ей исходную последовательность; эти пробелы отвечают либо делециям букв в этой последовательности, либо вставкам букв, произошедшим в каких-то других последовательностях исходного набора. При этом на некоторых участках набора выравненных последовательностей между всеми или некоторыми его слоями существует сходство. Такие участки будем называть “консенсусами”. Степень сходства между слоями консенсуса характеризуется его мощностью, которая вычисляется как нормированная сумма весов за попарные замены остатков (букв), стоящих в одном столбце консенсуса:
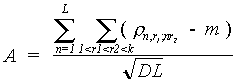
где А — мощность рассматриваемого консенсуса;
L — длина консенсуса, т. е. общая длина входящих в него фрагментов; k — толщина консенсуса, т. е. число входящих в него слоев; b1r, b2,r, ... , bL,,r — буквы (остатки), составляющие r-й слой консенсуса; r b,c— вес за замену буквы b набукву с (для белков эти веса обычно берутся из матрицы Дэйхофф [6]);
т = М
(r ) = å r b, c • pb • рс — (2) b,ссреднее значение веса за замену букв (суммирование в (2) производится по всевозможным буквам алфавита; для белков их 20);
D = k· (k- l)/2 · D (r ) + k · (k- l) · (k-2) · cov(r 12 ,r 13)=
= k· (k- l)/2 · å ( r b, c - m)2 • pb • рс + k · (k- l) · (k-2) x
b,с
x å ( r b, c1 - m) • ( r b, c2 - m)• pb • рс1 • рс 2 ;
b,с1,c2pb— частота буквы bво всем наборе последовательностей.
Для случая консенсуса толщины два обоснование этого определения приведено в [5]. Следует сказать, что формула (1) несколько огрублена по сравнению с аналогичной формулой в [5]: в формуле (1) частоты вхождения букв рь предполагаются одинаковыми для всех выравниваемых последовательностей. Это сделано для ускорения времени счета; такое огрубление слабо влияет на точность оценок мощности консенсусов.
Заметим, что для поиска функционально важных участков знание консенсусов, по-видимому, даже более важно для биолога, чем само выравнивание. Поэтому процедура поиска консенсусов имеет самостоятельную ценность. В сущности, таким образом мы получаем многомерный аналог карты локальных сходств.
Из вышеизложенного вытекает, что при поиске правильного выравнивания естественно сначала находить все консенсусные участки без пробелов, а затем цепочку из таких участков достроить до полного выравнивания последовательностей, вставляя необходимое число пробелов в зонах между этими участками. При этом из биологических соображений ясно, что в правильном выравнивании родственных последовательностей, с одной стороны, консенсусы должны быть по возможности более мощными и, с другой — пробелов должно быть немного.
В соответствии с этим в нашем алгоритме выделяются два этапа:
Начнем с первого этапа.
Для нахождения всех возможных в данном наборе последовательностей консенсусов следовало бы просмотреть все “регистры сравнения” (возможные сдвиги исходных последовательностей относительно друг друга) и для каждого из них искать совокупность непересекающихся достаточно мощных консенсусов, что можно сделать, например, с помощью программы DotHelix [5]. Однако такая процедура требует даже при сравнительно небольшом числе последовательностей (t³ 3) весьма большого времени счета, поскольку велико число разных регистров сравнения — оно порядка пt-1, где п — средняя длина последовательности. Чтобы избежать полного перебора всех регистров сравнения, предлагается использовать последовательную процедуру нахождения наиболее мощных консенсусов. Эта процедура основана на том обстоятельстве, что в мощном консенсусе каждая или почти каждая пара слоев значимо похожи.Соответствующий алгоритм заключается в следующем. Для каждой пары последовательностей из набора методом
DotHelix находим все сходные фрагменты этих последовательностей на сравнительно низком уровне значимости. Тем самым будут найдены все достаточно мощныеконсенсусы толщины два. Далее происходит постепенное утолщение консенсусов: консенсусы толщины три получаются из консенсусов толщины два, консенсусы толщины четыре получаются из консенсусов толщины три и т. д. за счет поочередного подцепления к каждому из них подходящих фрагментов очередной последовательности. Таким образом, каждый консенсус как жесткое целое сдвигается вдоль всех незадействованных в этом консенсусе последовательностей и присоединяет к себе в качестве дополнительного слоя подходящие фрагменты.
Опишем более подробно процедуру присоединения нового слоя. Ее проводили методом
DotHelix [5], но по несколько другим правилам вычисления мощности (которую мы будем называть “мощностью подцепления”) . Консенсус, продолженный в обе стороны на несколько позиций, сдвигается относительно сравниваемой последовательности, и для каждого сдвига формируется диагональ карты локального сходства консенсуса и этой последовательности (для сравнения см. [5]); числа аi,j , заполняющие карту локального сходства, являются суммами весов за замены букв из i-го столбца консенсуса на букву из j-й позиции сравниваемой последовательности: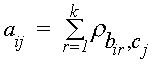 ,
,
где
k — число слоев консенсуса, bir — буква, стоящая в r-м слое i-м столбце консенсуса, сj — буква, стоящая в j-й позиции сравниваемой с консенсусом последовательности, рb,с — вес за замену буквы b на букву с. Как было указано выше, формула для мощности подцепления несколько отличается от приведенной выше формулы (1) для мощности консенсуса. Это связано с тем, что слои консенсуса нельзя рассматривать как независимые бернуллиевские последовательности (например, вполне реальная ситуация, когда все слои консенсуса в точности совпадают между собой). Поэтому консенсус следует рассматривать не как набор случайных, а как набор фиксированных последовательностей, состоящих из букв bi,r. В то же время вполне естественно представлять сравниваемую последовательность бернуллиевской и независимой от слоев консенсуса. В результате вместо формулы (1) мощность подцепления следовало бы вычислять так: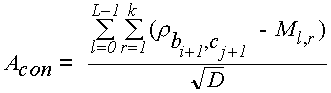
где
L — длина отрезка диагонали, мощность которого мы вычисляем;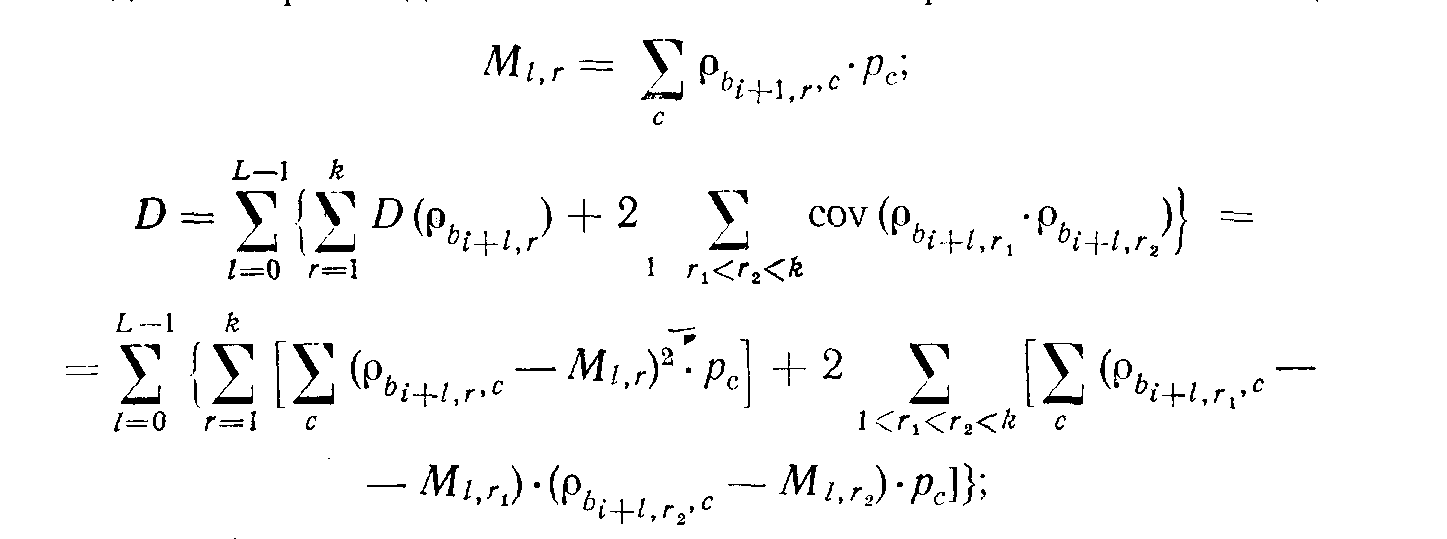
pc —частота буквы с.
К сожалению, вычислять по этой громоздкой формуле приходится очень часто, а это самым пагубным образом сказывается на скорости счета. Поэтому в программе используется оценка мощности подцепления по приближенной формуле. Эта оценка исходит из следующих предположений (которые, безусловно, являются лишь приблизительными) : во-первых, что частоты букв в консенсусе такие же, как во всех последовательностях в совокупности; во-вторых, зависимость между слоями консенсуса выражается только в увеличении количества совпадений букв в его столбцах. Первое предположение приводит к тому, что Мrl тождественно равно т, в силу же второго предположения имеет место формула
D
= L{(k + neq)· å (r b,c-m)2· pb· pc + [k.(k-1)-neq] xxå (r b1,c - m)· (r b2, c - m)· pb1· pb2· pc.
Здесь
neq характеризует степень согласованности в столбцах консенсуса (по сравнению с той, которая была бы для случая бернуллиевских и не-зависимых между собой слоев), переведенную в ожидаемое число совпадений букв в столбце (точнее говоря, увеличение этого числа совпадений по сравнению со случаем независимых слоев).Мы вычисляем эту величину
neq исходя из мощности консенсуса, предполагая, что такое значение мощности и соответствующее значение нормированной суммы весов (стоящей в числителе формулы (1)) про-исходит только за счет точных совпадений букв (конечно, и это пред-положение является лишь приближенным); из этого предположения легко следует, что
neq = S / (meq - m)· L ,
где
meq = å r b,b— среднее значение весов r ь ь , т вычисляется по формуле (2,b
S — нормированная сумма весов для консенсуса, получаемая из значения его мощности (см. формулу (1)).
При процедуре присоединения нового слоя мы отбираем только те новые консенсусы, мощность подцепления для которых выше некоторого порога.
В результате всей этой работы мы получим некоторую совокупность консенсусов разной толщины; каждому консенсусу соответствует его мощность, рассчитанная уже по формуле
(1). Неполная толщина консенсуса в окончательном наборе означает, что входящие в него последовательности заведомо имеют хорошее соответствие между собой в этом месте; что же касается пропущенных в этом консенсусе последовательностей, то хорошего соответствия со слоями консенсуса там нет.Промежуточное хранение консенсусов (для экономии памяти и времени счета) осуществляется по принципу “стека” так, что сохраняется определенное число наилучших по мощности. При построении очередного консенсуса набор переупорядочивается и худший выталкивается из стека.
Говоря метафорически, в предложенном нами
способе поиска консенсусов из рассмотрения всевозможных пар последовательностей намечаются потенциальные зоны сходства, а потом некоторые из них все более проявляются за счет сходств этого участка с фрагментами из других последовательностей, а другие стираются ввиду отсутствия дополнительных сходств.При вышеописанном способе получения консенсусов довольно большое количество их будет шумом, мешающим последующему построению выравнивания из этих консенсусов (увеличивается перебор).
Это обстоятельство в основном связано с нашей нулевой гипотезой о независимости выравниваемого набора последовательностей, хотя само желание их выравнить предполагает обратное. Очевидно, что для зависимых (в сторону возможности выравнивания) последовательностей среднее значение М(r ) весов за замену букв увеличивается по сравнению с формулой (2). В нашей программе имеется возможность учесть это обстоятельство, увеличивая величину т. Эксперименты показывают, что такая процедура отфильтровывает значительное количество шумовых консенсусов. Однако вопрос об оптимальном наборе величины т нуждается в дальнейшем изучении.Перейдем теперь к описанию второго этапа — построению наилучших выравниваний из консенсусов.
После выделения полного набора достаточно мощных консенсусов нужно искать все возможные комбинации их состыковки, причем для составления полного выравнивания, кроме пробелов, придется использовать и “неконсенсусные” участки. Поскольку трудно ожидать, что в биологических последовательностях существует значимое “отрицательное” сходство с отрицательной мощностью, т. е. маловероятное с позиций случайности несходство, можно думать, что порядок расположения букв и пробелов в неконсенсусном участке не очень существен. В пашем алгоритме в неконсенсусных участках по каждому слою сначала идут буквы, а затем добавляется необходимое число пробелов.
В случае наложения двух консенсусов из разных регистров (т. е. в случае, когда эти консенсусы содержат хотя бы один общий фрагмент какой-либо последовательности, входящей в оба
эти консенсуса) с помощью вставки необходимого числа пробелов можно перейти от одного консенсуса к другому. Этот переход осуществляется у нас в том месте, которое обеспечивает наибольшее значение суммарной мощности.Как было уже сказано, выбор выравнивания состоит в построении согласованной по порядку букв в последовательностях цепочки консенсусов. При этом для уменьшения перебора таких цепочек все найденные консенсусы разделяются на несколько групп по мощности (всего возможно не более десяти групп). После этого вначале составляются все возможные цепочки из сравнительно небольшой группы самых мощных консенсусов, затем в эти цепочки всеми возможными способами вставляются консенсусы из следующей группы по мощности и т. д. до исчерпания всех групп.
В итоге мы получим набор выравниваний с максимально возможным включением в каждый из построенных на первом этапе консенсусов (максимальность понимается в том смысле, что цепочки насыщены — больше добавить туда консенсусов нельзя). Мерой качества выравнивания служит нормированная сумма попарных весов за замены букв из всех столбцов консенсусов соответствующей цепочки (сравни с формулой
(1); в качестве длины L берется общая длина выравненных последовательностей) . Видно, что при таком определении хорошее качество имеют такие выравнивания, в которые по возможности входят мощные консенсусы при небольшом числе вставленных пробелов.После получения выравнивания пользователь имеет возможность вручную поправить его, выкинув из исходного набора тот консенсус, включение которого в цепочку заставляет сильно увеличить число вставленных пробелов и затем с новым набором консенсусов вновь проделать процедуру составления цепочек.
Окончательный выбор наилучшего выравнивания можно осуществить разными способами. Например, такое наилучшее из набора найденных с разным числом пробелов может выбирать пользователь. Можно также использовать то обстоятельство, что для того значения числа пробелов, при котором имеет место “истинное” выравнивание (восстанавливающее предковую последовательность, если таковая существует), должно резко подскочить нормированное значение суммарной мощности консенсусов.
Данный алгоритм реализован на языке Си для компьютеров типа
IBM PC в виде программы H-Align из пакета программ для анализа последовательностей биополимеров GenBee, разработанного в НПК “Комби”.Результаты и обсуждение. В качестве проверки работоспособности алгоритма мы исследовали следующий модельный пример. Были взяты четыре последовательности цитохромов С из разных животных — шимпанзе, собаки, индейки и утки (последовательности—“прародители”). Они очень похожи и состоят из 104 аминокислотных остатков. Далее их
“мутировали”: около
45% букв было заменено дефисами — символами “—”. На следующем шаге все дефисы были убраны. В результате получились более короткие последовательности с длинами 43, 53, 66 и 75 букв. Эти последовательности и взяты как исходные для выравнивания. Схема модели приведена на рис. 1.Результаты работы по программе
H-Align представлены на рис. 2, где изображены два набора выравненных последовательностей, полученные с использованием разных матриц весов за замены остатков: матрицы Дэйхофф [6] и единичной матрицы (в ней вес за совпадение букв равен единице, а за несовпадение — нулю). В обоих изображенных наборах выравненных последовательностей большими буквами показаны места, входящие в консенсусы, а маленькими — в межконсенсусные участки.Последовательности -"прародители"
1:GDVEKGKKIFIMKCSQCHTVEKGGKHKTGPNLHGLFGRKTGQAPGYSYTAANKNKGIIWG 1:GDVEKGKKIFVQKCAQCHTVEKGGKHKTGPNLHGLFGRKTGQAPGFSYTDANKNKGITWG 1:GDIEKGKKIFYQKCSQCHTVEKGGKHKTGPNLHGLFGRKTGQAEGFSYTDANKNKGITWG 1:GDVEKGKKIPVQKCSQCHTVEKGGKHKTGPNLHGLFGRKTGQAEGFSYTDANKNKGITWG 61:EDTLMEYLENPKKYIFGTKMIPVGIKKKEERADLIAYLKKATNE 61:EETLMEYLENPKKYIPGTKMIFAGIKKTGERADLIAYLKKATKE 61:EDTLMEYLENPKKYIPGTKMIFAGIKKKSERVDLIAYLKDATSK 61:EDTLMEYLENPKKYIPGTKMIFAGIKKKSERADLIAYLKDATAK
"Мутированные" последовательности
1:----KGKKIF-------------GKHKTGPNLH------------------KNKGIIWG 1:GDV-KGKKIFVQK----TVEK--------NLHGLFGRKT---PGFSY----KNKGITWG 1:GD—KG----VQKCSQ—ТVEK-GКНKTGРNLH---GRKTG--—EGFS-----KNKGITWG 1:------KKIFVQKCSQ—TVEKG-----GPNLHG—GRKTGQAE-G---TDAN---GIT-G 61:-DTL--YLENPK-YIPGTKMIF--------RADLIAYLKKA--- 61:E--------------------------------LIA-------- 61:-DTL--YLEN----IPGTKMI--GIKKKSERVDLIAYLKDATS- 61:EDT--EYLEN----IPGTKMIFAGIKKKS-----------АТАК
Исходные для выравнивания последовательности
1:KGKKIFGKHKTGPNLHKNKGIIWGDTLILENPKYIPGTKMIFRAD LIAYLKKA 1:GDVKGKKIFVQKTVEKNLHGLFGRKTPGFSYKNKGITWGELIA 1:GDKGVQKCSQTVEKGKHKTGPNLHGRKTGEGFSKNKGITWGDTLYLENIPGTKMIGIKKK 1:KKIFVQKCSQTVEKGGPNLHGGRKTGQAEGTDANGITGEDTEYLENIFGTKMIPAGIKKK 61: 61: 61:SERVDLIAYLKDATS 61:SATAK
Рис. 1. Конструирование исходных для выравнивания последовательностей
На рис. 2, кроме результатов выравнивания по программе
H-Align, приведено также “истинное” выравнивание. Оно получается из образованных нами последовательностей с дефисами (второй набор последовательностей— на рис. 1) выбрасыванием столбцов, состоящих из одних дефисов.Сравнение трех выравниваний показывает, что все они достаточно хорошо соответствуют друг другу, однако выравнивание с использованием единичной матрицы более похоже на “истинное”. Это обстоятельство объясняется способом построения исходных последовательностей, в результате чего практически все соответствующие друг другу буквы “истинного” выравнивания совпадают между собой. Поэтому единичная матрица весов, стремящаяся выделить консенсусы с совпадением букв, больше подходит для выравнивания таких последовательностей, чем матрица Дэйхофф.
Кроме того, отметим, что в межконсенсусных участках места расположения дефисов указываются не вполне точно. Это объясняется тем,
что наш алгоритм действует по правилу сдвига всех таких мест в конец соответствующего участка. Однако на таких участках искать какое-либо соответствие невозможно (по крайней мере, без использования биологических соображений), поскольку наблюдаемое на них сходство между буквами находится на уровне случайного.Выравненные по матрице Дэйхофф последовательности
1:kg---KKIP----------GKHKTGPNLH--------------KNKGIIWGDTLYLENpky 1:gdvkgKKIFVQKtv---------- EKNLHglfGRKtpgfsy-KNKGITWGE--------- 1:gdkg-----VQKCSQTVekGKHKTGPNIH---GRKtgegfs--KNKGITWGDTLYLEN--- 1:-----KKIFVQKCSQTV----EKGGPNIHg—GRKtggaegtda-N-GITGEDTEYLEN--- 61:IPGTKMIfra--------DLIAYLKka-- 61:-------------------LIA------- 61:IPGTKMI--GIKKKservDLIAYLKdats 61:IPGTKMIfaGIKKKsatak----------
Выравненные по единичной матрице последовательности
1:kg---KKIP----------GKHKTGPNLH---------------KNKGIIWGDTLYLENpky 1:gdvkgKKIFVQK---TVEk-------NLHGlfGRKTpgfsy---KNKGITWGe--------- 1:gdkg-----VQKCSQTVEkGKHKTGPNLH---GHKIGegfs---KNKGITWGDTLYLEN--- 1:-----KKIFVQKCSQTVE----KGGPNLHG—GRKTGqaegtdan---GITgeDTEYLEN--- 61:IPGTKMIFra--------DLIAYLKka— 61:-------------------LIA------ 61:IPGTKMI—GIKKKServDLIAYLKdats 61:IPGTKMIFaGIKKKSatak---------
"Истинное" выравнивание
1:---KGKKIF-----------GKHKTGPNLH------------------KNKGIIWG-DT 1:GDVKGKKIFVQK---TVEK--------NLHGLFGRKT---PGFSY---KNKGITWGE-- 1:GD-KG----VQKCSQTVEK-GKHKTGPNLH---GRKTG—EGFS-----KNKGITWG-DT 1:-----KKIFVQKCSQTVEKG-----GPNLHG—GRKTGQAEG---TDAN---GIT-GEDT 61:L--YLENPK-YIPGTKMIF--------RADLIAYLKKA--- 61:------------------------------LIA-------- 61:L--YLEN----IPGTKMI--GIKKKSERVDLIAYLKDATS- 61:--EYLEN----IPGTKMIFAGIKKKS-----------АТАК
Рис. 2. Результаты выравнивания по программе
H-Align исходных последовательностей с использованием разных весовых матриц (Дэйхофф и единичной), а также “истинное” выравниваниеРезюме
У роботi запропоновано новий алгоритм множинного вир
iвнювання бiологiчних по-слiдовностей. В ньому спочатку на основi методу DotHelix будуються консенсуснi дiлянки в даному наборi послiдовностей piзнoi товщини i ступеня схожостi, а потiм iз цих консенсусiв складаються ланцюжки, погодженi з порядком букв в послiдовностях, i такi ланцюжки е каркасами вирiвнювання. На основi алгоритму на мовi Сi написана програма H-Align з пакету GenBee. Розглянутий модельний приклад iлюструе ефективнiсть запропонованого алгоритму.Summary
Generalization of the multiple alignment is central to the entire field of biological sequence analysis. The algorithm of alignment by program H-align incorporated in GenBee package is a result of development of the local similarity search principle. It has two stages:
1) generalization of all the conservative regions (they cannot be present in all the aligning sequences).
2) optimal arrangement of these regions using two criteria — maximization of the total power of the conservative regions and minimization of the total number of spaces.
This algorithm has at least two advantages over traditional algorithms (such as Needleman-Wunsch's one) : no penalty for insertion / deletion; not subsequent pair aligning procedure. The efficiency of the algorithm is shown at model example.
СПИСОК ЛИТЕРАТУРЫ
1. Needleman S. В., Wunch C. D. A general method applicable to the search for similarities in the amino acid sequence of two proteins//J. Mol. Biol.— 1970.— 48, N 2.— P. 443—453.
2. Gotoh O. Alignment of three biological sequences with an efficient traseback procedure//J. Theor. Biol.—1986.—121, N 1.—P. 327—337.
3. Sobel E., Marttinez H. M. A multiple sequence alignment program//Nucl. Acids Res.— 1986.— 14, N 2.—P. 363—374.
4. Bacon D. /., Anderson W. J. Multiple sequence alignment//J. Mol Biol.— 1986 — 191, N 1.—P. 153—161.
5. Леонтович A. M., Бродский Л. И., Горбаленя А. Е. Построение полной карты локального сходства двух полимеров (программа DotHelix пакета GenBee // Биополимеры и клетка.— 1990.—6, № 6.—С. 14—21.
6. Dayhoff M. О., Barker W. С., Hunt L. Т. Establishing homologies in protein sequences //Meth. Enzymol.— 1983.— 91.— P. 524—545.
Науч.-произв. кооператив “Комби”, Москва Получено 28.06.90
Межфакультет. н.-и. лаб. им. А. Н. Белозерского, МГУ